Aufgabe A 2.1
An einem Stausee wird der Zu- und Abfluss künstlich geregelt.
Dabei wird die momentane Zuflussrate beschrieben durch die Funktion z mit
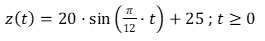
a(t)=19; t≥0
(t in Stunden seit Beobachtungsbeginn, z(t) und a(t) in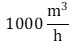 ).
).a) Zunächst werden die ersten 24 Stunden nach Beobachtungsbeginn betrachtet.
Bestimmen Sie die minimale momentane Zuflussrate.
In welchem Zeitraum nimmt die Wassermenge im Stausee ab?
Bestimmen Sie die maximale momentane Änderungsrate der Wassermenge.
(4 VP)
b) Zu Beobachtungsbeginn befinden sich 2 500 000 m³ Wasser im See.Bestimmen Sie die Wassermenge im Stausee 12 Stunden nach Beobachtungsbeginn.
Begründen Sie, dass die Wassermenge in jedem 24-Stunden-Zeitraum um 144 000 m³ zunimmt.
Welchen Wert müsste die konstante Abflussrate haben, damit nach Ablauf von 14 Tagen die Wassermenge im Stausee 4 180 000 m³ betragen würde?
(5,5 VP)
Aufgabe A 2.2
Gegeben ist die Funktion f mit f(x)=x3-9x2+24x-14.
a) Die Gerade g durch den Hochpunkt H und den Tiefpunkt T des Graphen von f schneidet die Koordinatenachsen in den Punkten P und Q.
Bestimmen Sie den prozentuellen Anteil der Strecke HT an der Strecke PQ.
(4 VP)
b) Begründen Sie, dass die Steigung des Graphen von f keine Werte kleiner als -3 annehmen kann.(2 VP)
c) Der Graph von f und die Gerade h mit der Gleichung y=2 schließen eine Fläche ein. Diese Fläche rotiert um die Gerade h. Berechnen Sie das Volumen des entstehenden Rotationskörpers.(2,5 VP)
d) Eine Parallele zur x-Achse schneidet aus dem Graphen von f ein Kurvenstück aus, das den Tiefpunkt enthält.Die Endpunkte dieses Kurvenstücks haben den Abstand 2,5 voneinander.
Bestimmen Sie eine Gleichung dieser Parallelen.
(2 VP)